Lesson 14: Recursion

This is the song that doesn't end
It just goes on and on, my friend
Some people started singing it not knowing what it was
And they'll continue singing it forever just because
This is the song that doesn't end...

“The Song that Doesn’t End” illustrates recursion (also known as “Do unto others what was done unto you”), in that it invokes itself.

In computing, recursion refers to the case of a method calling itself (method a calls method a) repeatedly, or a series of methods (a calls b calls a calls b…) cycling back to the first method repeatedly.

Aside from driving Shari Lewis bonkers, recursion is useful whenever you want to repeat a process on some object’s successor(s) that was performed on the object itself. Confusing? Let’s take the classic example: to find the factorial of an integer, multiply that integer by the factorial of the integer that’s one less. To get 4!, you multiply 4 by 3!, which you get by multiplying 3 by 2!….

    4! = 4 x (4 - 1)!
    3! = 3 x (3 - 1)!
    2! = 2 x (2 - 1)!

To find a factorial, we can code a method we’ll call bang().

“bang” is a printer’s term for an exclamation point, the mathematical symbol for a factorial. Yes, we know it has another meaning.

    public int bang(int startValue) {
        if (startValue == 0) {
            return 1;
        }

        return startValue * bang(startValue - 1);
    }

Recursion is also useful for visiting all the nodes of a tree structure, such as finding all the files in your computer’s file system.

1. Set the “current” directory to the root node.
2. Look at each entry in the current directory.
3. If the entry is a directory, set the “current” directory to that and return to step (2).
4. If the entry is a file, add it to your collection of files.

The Stack

Every time you call a method, memory is allocated for all its fields from the stack. Not a stack–the stack. Each Thread in your JVM has only one (there’s a lesson on Threads coming up). When the method needs to access a field, it goes x number of bytes into the stack to reach it. And when the method returns, all the memory allocated for it is popped off the stack to reveal the memory belonging to whoever called that method.

We mention this because the stack is limited. When coding a recursive method, it’s vital that it have a way of escaping without calling itself again; this is called the base case. In bang(), that happens when the value passed is 0. Without such an escape hatch, the method calls itself indefinitely until the stack runs out of room; this leads to a StackOverflowError.

Admittedly, all this allocating and deallocating adds to your program’s overhead. Using recursion to find factorials is really rather silly. From an efficiency standpoint, it makes more sense to just write a loop:

    public int bang(int startValue) {
        int factorial = 1;
        for (int i = startValue; i > 0; i--) {
            factorial = factorial * i;
        }
        return factorial;
    }

Recursion is controversial; some developers maintain it should never be used. Yes, it’s possible to traverse your file system without it, and using recursion to find factorials is, as mentioned above, bonkers.

But for building or traversing a tree structure, or for finding permutations, looping is entirely too messy, and recursion is the way to go.

We invite you to check out this video for some of the pitfalls of recursion.

A True Life Example

Here’s situation your humble correspondent faced in an actual project.

A relational database system (RDBMS) is composed of tables, which correspond to Java classes in that a table represents a type of entity. The “relational” aspect is that one table can be related to another one, often in a hierarchy. Consider this one:

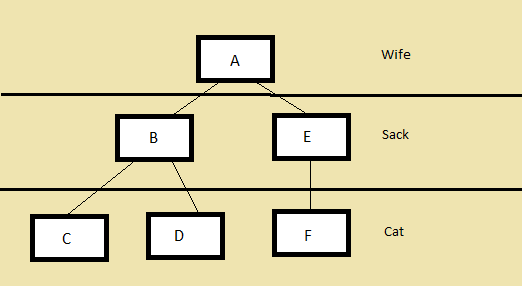
In this database, each Wife has zero or more Sacks, and each Sack has zero or more Cats. Well, suppose the Man (not shown) divorces Wife A (he has six others), and we want to remove her from the database. If our database employs referential integrity, as many do, before we can remove Wife A, we have to remove Sacks B and E that depend upon her. And before we can remove Sacks B and E, we have to remove the Cats that depend upon them.

This becomes a recursive process which might look something like this:

public class Wife {
    public void delete() {
         for (Sack s : this.getSacks()) }
            s.delete();
         }
         deleteMe();
    }
}

public class Sack {
    public void delete() {
         for (Cat c : this.getCats()) }
            c.delete();
         }
         deleteMe();
    }
}

public class Cat {
    public void delete() {
         deleteMe();
    }
}

Strictly speaking, this isn’t recursion in that none of the delete() methods calls itself. But you can see the resemblance to actual recursion. The process of deleting a Wife entails first deleting her Sacks, and the process of deleting a Sack entails first deleting its Cats, and execution plunges deeper and deeper into the hierarchy before resurfacing and an entity can delete itself.

Exercise

Write a program to accept a string from the console, shift it to uppercase, and print all distinct permutations of its characters (prefaced by how many permutations there are). You’ll want to use recursion to do this. Keep the string short so you can appreciate the output, and to avoid a StackOverflowError.

Here is code to accept input from the console. You terminate your input by pressing Enter.

        Reader rdr = new InputStreamReader(System.in);
        BufferedReader br = new BufferedReader(rdr);

        System.out.print("Enter letters: ");
        String line = br.readLine();

The sample solution (downloadable here) contains two main classes. ScrambleSimple uses StringBuilders to accomplish the task. ScrambleTree builds and traverses a tree structure, using recursion for both processes. (Building and maintaining a tree is typically a recursive process.) We suggest you pay particular attention to ScrambleTree because tree structures are used a lot in IT.

What You Need to Know

Now let’s take a look at Reflection.